|
華信電子週報 <不動產行情、不動產估價、不動產法規類> |
||||||||||
前言:前篇針對特徵價格理論做說明。本期電子報針對何謂特徵價格模型於房價研究上之應用做說明,如有錯誤或遺漏之處,尚請不吝指正,謝謝!
多元線性迴歸模式主要是在探討可觀察變數(Manifest Variable )與潛在變數(Latent Variable)間的線性關係及各潛在變數(Latent Variable )間之因果關係。所以可以同時完成評估系統的測量問題與因果關係式(潛在變數間的關係)。 多元線性迴歸模式(multiple linear regression model)的一般式可定義如下: Y=α+β1 X1+β2 X2+β3 X3+….+βk Xk+ε 上述模型的假設如下: (一)Y為應變數,是需要被預測的變數。 (二) α、β1、β2、β3、….、βk為未知常數。 (三) X1、X2、X3…. 、Xk為自變數、是用來預測的變數,沒有誤差。 (四)ε是隨機誤差、在X1、X2、X3…. 、Xk固定的情況下,ε為期望值0與變異數σ2的常態分配。 (五)不同Y值所對應的隨機誤差ε彼此獨立。
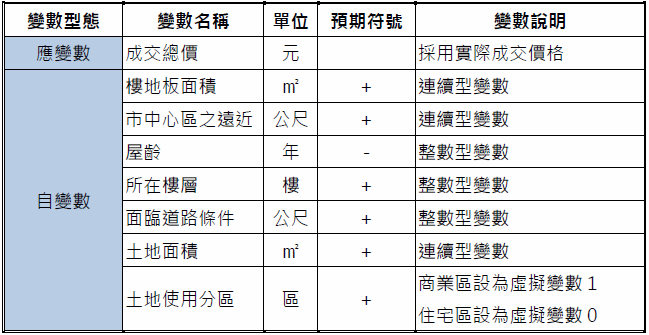
(一)應變數:而自西元2012年起實價登錄制度正式上路後,現階段公開資訊已趨近於完善,對於民眾在購屋上具一定程度上的參考價值,因此採用實際成交價格作為模型之應變數。 (二)自變數:對於不動產價格影響之變數,假設以樓地板面積、市中心區之遠近、屋齡、所在樓層、面臨道路條件、土地面積、土地使用分區等各項自變數。
採現多元線性迴歸模式,是以商品的各個特徵屬性乘上相對應的隱含價格後之總和,即為該產品的價格,依據前述理論模型,及前述假設各項隱含之特徵,建構出下列線性函數: Y=α+β1 X1+β2 X2+β3 X3+β4 X4+β5 X5+β6 X6+β7 X7+ε Y:為住宅大樓實際成交價格(元)。 X1:樓地板面積(㎡):依成交標的交易紀錄所標示之面積。 X2:市中心區之遠近:以台中火車站為市中心之直線距離(公尺)。 X3:建物屋齡(年):依成交日期與建築完成日期之時間計算。 X4:標的所在樓層:依成交標的所在樓層標示。 X5:面臨道路條件:依成交標的實際面臨之道路寬度。 X6:土地使用分區:商業區設為虛擬變數1;住宅區設為虛擬變數0。 X7:土地面積:依成交標的實際成交所持分之土地面積。 βi:各種特徵所隱含之價格。 ε:殘差項。
藉由這2篇電子報分享特徵價格模型於房價研究上採用之多元線性迴歸分析,後續再延伸說明不動產估價技術規則第20條。
|
||||||||||
|
|




 留言列表
留言列表


